
【作者】Ruoxi Wanga, Qi Wangc, Nan Lia,b
a Department of Construction Management, Tsinghua University, China
b Hang Lung Center for Real Estate, Tsinghua University, China
c Department of Civil and Environmental Engineering, Northeastern University, Boston, United States of America
【通讯作者邮箱】nanli@tsinghua.edu.cn
【期刊信息】Sustainable Cities and Society, Volume 91(2023) 104435
【全文链接】https://doi.org/10.1016/j.scs.2023.104435
摘要
城市人群移动可能会受到各种极端事件的严重干扰。这些干扰威胁着城市空间连通性,并影响人们获取各种基本服务的能力。准确描述城市人群移动网络的相变状态并及时发出警报,有助于缓解上述风险。然而,目前缺乏一种方法来表征城市移动网络的相变状态并在极端事件期间发出预警信号。同时,现有城市人群移动网络的渗流分析缺乏在不同城市的对比,相关结论的普遍适用性尚未得到充分验证。通过挖掘大规模人群时空定位数据,我们构建了美国人口排名前50的大都市统计区(MSAs)的人群移动网络,并通过网络渗流分析探索它们受到扰动后的响应模式。结果表明,美国50个城市的人群移动网络均产生了关键转变现象,在对城市人群移动网络中的流量进行归一化处理后,不同城市人群移动网络的关键临界点存在高度一致性,证实了结论的普遍适用性。接着,我们基于网络中簇大小的概率分布设计了预警指标,用来近似衡量人群移动网络当前状态与临界阈值的距离,从而为其相变提供早期预警。上述研究为人群移动网络中的关键状态转换提供了预测工具,通过预测人群移动网络何时接近相变点和发生网络裂解的现象,可以指导风险评估和灾害情景规划等工作,维持人群移动网络的高度连通性。
关键词: 人群移动网络;渗流分析;网络相变;预警指标
方法
本研究基于SafeGraph提供的2019年美国人口普查区组(CBG)层级的人群移动数据集,衡量了以天为时间颗粒度的人口普查区组之间的人群移动流量。为验证结论的普遍适用性,我们基于总人口排名,提取了美国人口排名前50的大都市统计区(MSA)的人群移动数据用于分析。
进行渗流分析时,首先需要确定每个大都市区内的CBG之间的交互强度。在这里,我们使用从移动数据中得出的标准化加权人群移动流量来表征CBG之间连接的强度。然后,每个CBG都被视为一个节点,使用交互强度作为权重创建CBG之间的无向有权边。在渗流过程中,依据权重阈值q移除权重低于此阈值的连边。最后,在每次连边移除后计算网络中的最大连通子图(GC)和第二大连通子图(SGC)的大小以评估网络连通性。
研究发现
(1)人群移动网络的渗流过程
图1以9个MSAs为例展现了渗流过程,绘制了渗流过程中GC(蓝线)和SGC(红线)的动态变化。每个子图中的两个地图显示了在临界阈值qc之前和之后的GC(蓝色区域)的大小。
所有的城市人群移动网络在渗流过程中均表现出了相同的模式:城市移动网络在扰动增加(邻域间移动减少)的情况下变得脆弱,并在临界点qc处突然发生相变。具体而言,随着q的增加,GC逐渐变小,而SGC逐渐增大。在qc处,SGC达到最大值,GC呈现出剧烈的收缩,意味着人群移动网络在此刻发生相变。
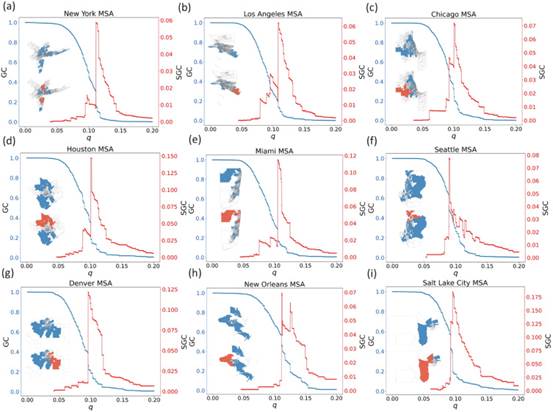
图 1:9个案例城市中人群移动网络的渗流曲线
(2)人群移动网络的普遍性模式
尽管不同都市统计区在地理属性、人口密度、移动网络拓扑结构等方面具有多样性,我们观察到,在50个都市统计区中人群移动网络遵循高度相似的渗流过程。这些网络的GC在连边移除的开始时保持稳定,随着q的不断增加,GC开始缩小,最终达到零(图2)。有趣的是,从50个都市统计区的每日移动网络中提取出的qc值分布在一个狭窄的范围内并遵循正态分布(图3),其均值为0.096,仅具有0.012的标准差(KS检验,p值=0.905)。该发现揭示了不同的都市统计区的人群移动网络在渗流过程中的临界阈值上的高度一致性。
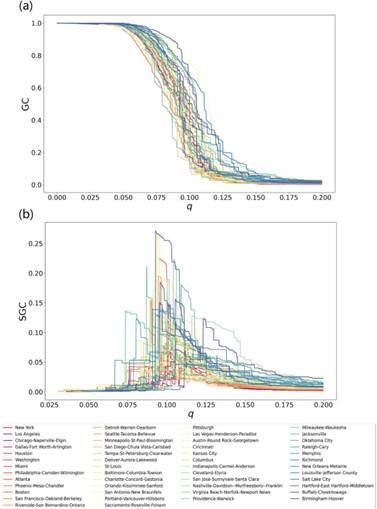
图 2:美国50个大都市区的渗流曲线(GC和SGC)
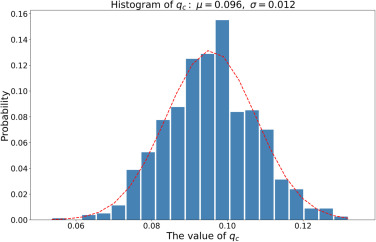
图 3:临界阈值的正态分布
(3)网络中簇大小的幂律分布
图4显示了50个MSA的人群移动网络在qc时(也即发生相变时)的簇大小分布,每种颜色代表不同的MSA。结果显示,50个MSA在相变点时网络中簇的大小全都遵循幂律分布。进一步地,人群移动网络在渗流临界点之前、附近、相变发生时和之后的簇大小分布如图5所示。在渗流过程中,当q接近qc时,所有MSA的人群移动网络中簇大小的分布逐渐趋向幂律分布。
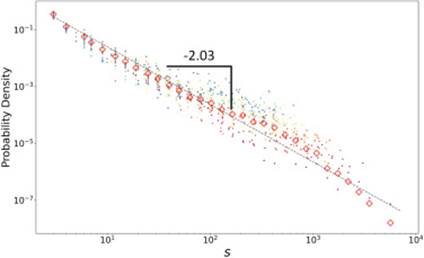
图 4:临界阈值处簇大小的正态分布
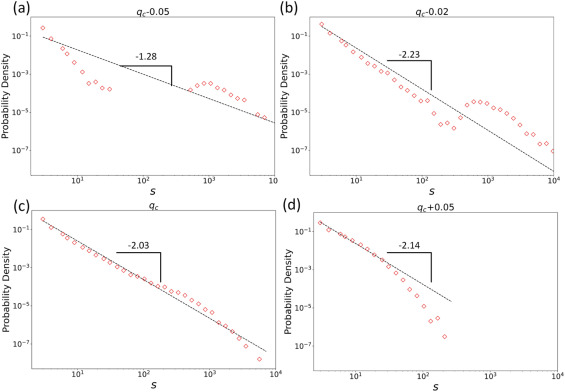
图 5:渗流过程中簇大小的概率分布
(4)预警指标设计
人群移动网络中簇大小的分布在相变点之前逐渐趋向幂律分布的现象为预警指标的设计提供了基本思路。人群移动网络相变的预警指标包含两部分内容。首先,计算Kolmogorov-Smirnov距离:
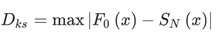
以量化人群移动网络簇大小的经验分布函数与拟合幂律分布的累积分布函数之间的距离。
然后,计算每个MSA 的Dks关于q的导数,表示为m:
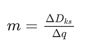
每个MSA网络中簇大小分布的Dks(图6(a))展现出临界相变前的显著下降趋势,反映了网络中簇大小分布和拟合幂律分布之间相似度的显著增加。预警指标m在渗流过程开始时远离零值,但随着q值接近渗流临界点,迅速趋近于零(图6(b))。m在渗流临界点前趋近于零的显著趋势,通过指示着在渗流相变前移动网络中无标度空间特征的出现,预警人群移动网络到其相变点的距离。
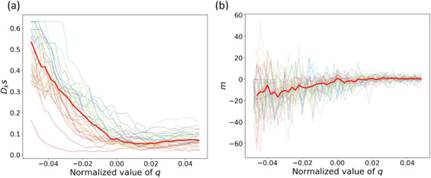
图 6:K-S距离和预警指标m在渗流过程中的变化
讨论和结论
了解和预警城市人群移动网络的关键状态转变,可以为应急干预策略的设计提供关键参考。 基于对美国50个大都市区人群移动网络的渗流分析,我们首先发现了两个跨城市背景的普适性结论:(1)50个大都市区相变的临界阈值qc遵循正态分布,表明这些大都市区在qc = 0.096左右具有相似的临界阈值;(2)人群移动网络中的簇大小均在临界相变点呈现出幂律分布。这些结论具有显著的理论和实践意义,不同城市在渗流模式呈现出的高度一致性,为具有普适性的管理措施的推行推广提供了有力支撑。人群移动网络的渗流分析不仅可以用于评估人群移动网络的韧性特征,还可以为城市管理实践中的应急管理提供启示,例如在流行病、冬季寒潮和暴雨等情况下,基于渗流过程识别关键连接、脆弱节点和高连接聚类,指导灾害中对关键连接进行保护以及灾难恢复期间重建连接的优先级。
此外,本研究提出了基于网络中簇大小分布的量化预警指标,可以用作人群移动网络相变的警示信号,用于警示移动网络接近其相变点的程度。该预警信号在美国50个大都市区收集的数据上进行评估,对于不同的城市均表现出良好的普适性,对于通过改进城市连通性的风险评估和制定有效的连通性保护措施具有重要意义。例如,预警信号可以提前告知政策制定者哪些社区有可能失去连通性,以采取针对性的措施,如改善公共交通、保障风险人群的出行能力、确保他们在极端事件期间获得基本生活资源和服务的能力等。